队列的概念
介绍完栈之后,接下来我们要介绍的是另一种跟栈很相似的数据结构 —— 队列。
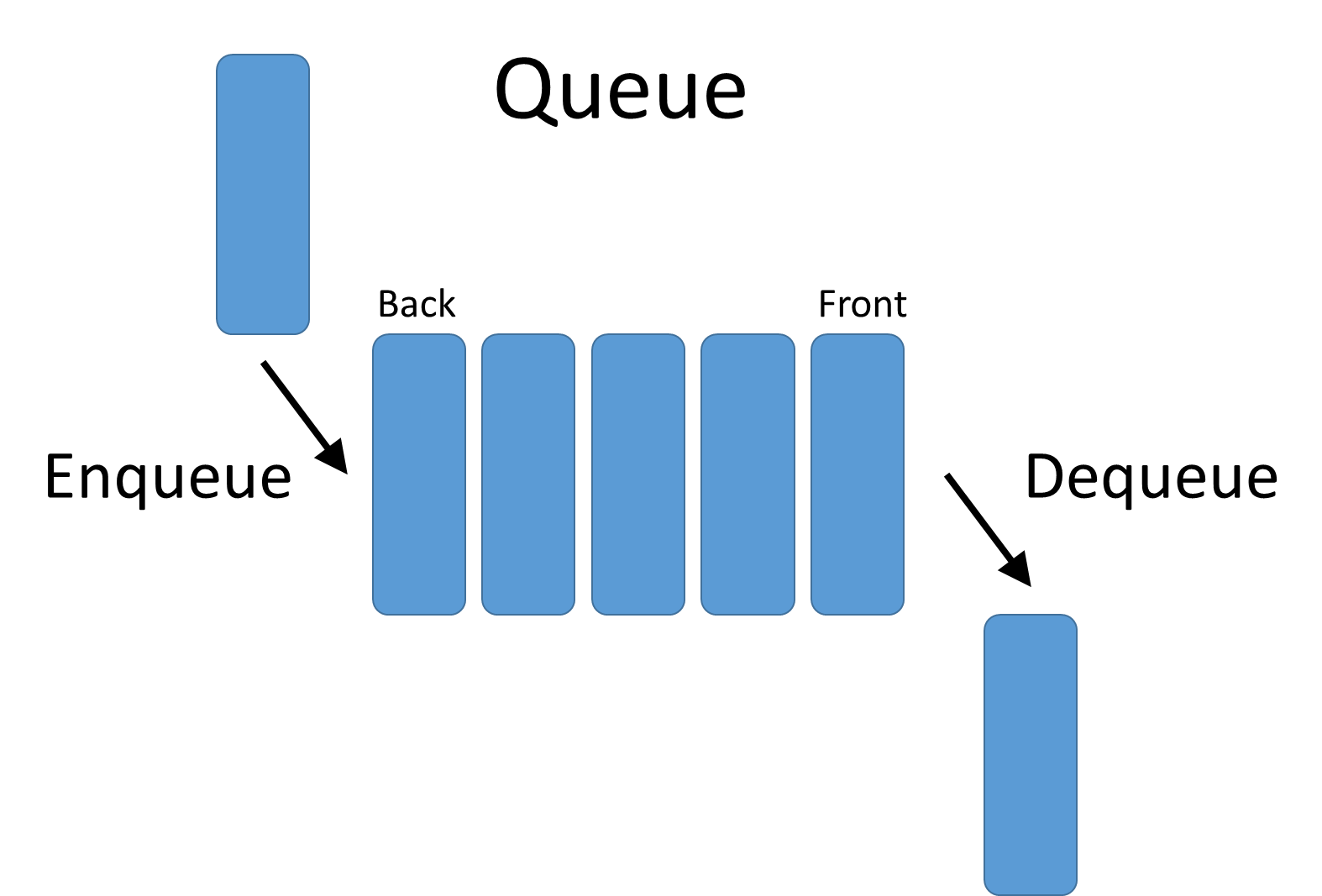
和栈一样,队列也是一种特殊的线性表结构,只不过队列是在一端插入,另一端删除,就跟我们平常排队一样的道理,从队尾入队,在队头出去,所以队列的特性是先入先出(FIFO),允许插入的一端叫队尾,允许删除的一端叫队头。
一张图可以形象地体现两者的差别:
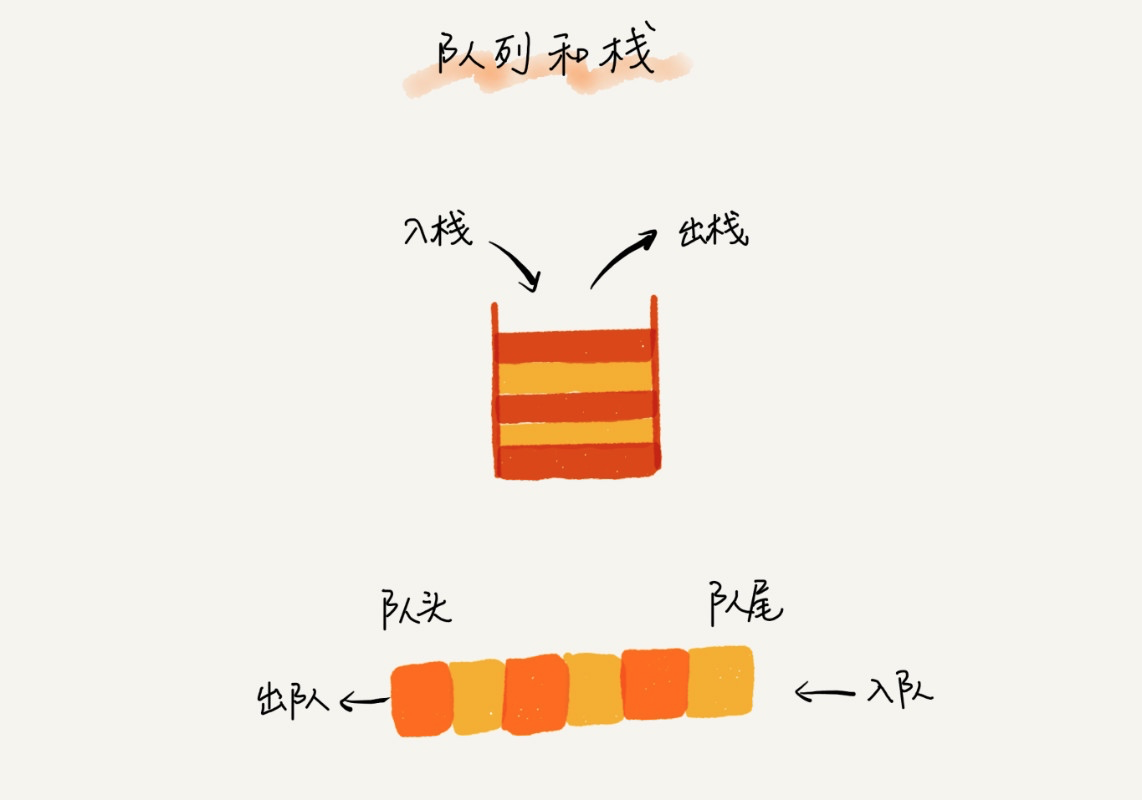
和栈一样,队列也可以通过数组和链表实现,通过数组实现的叫顺序队列,通过链表实现的叫做链式队列,栈只需要一个栈顶指针就可以了,因为只允许在栈顶插入删除,但是队列需要两个指针,一个指向队头,一个指向队尾。
队列的实现
基于链表实现队列的示例代码
下面我们以链式队列为例,看看如何通过 Go 代码基于链表实现队列这种数据结构,这里我们为队列提供了入队、出队和遍历三种操作:
package main
import (
"fmt"
)
// 定义链表节点
type Node struct {
Value int
Next *Node
}
// 初始化队列
var size = 0
var queue = new(Node)
// 入队(从队头插入)
func Push(t *Node, v int) bool {
if queue == nil {
queue = &Node{v, nil}
size++
return true
}
t = &Node{v, nil}
t.Next = queue
queue = t
size++
return true
}
// 出队(从队尾删除)
func Pop(t *Node) (int, bool) {
if size == 0 {
return 0, false
}
if size == 1 {
queue = nil
size--
return t.Value, true
}
// 迭代队列,直到队尾
temp := t
for (t.Next) != nil {
temp = t
t = t.Next
}
v := (temp.Next).Value
temp.Next = nil
size--
return v, true
}
// 遍历队列所有节点
func traverse(t *Node) {
if size == 0 {
fmt.Println("空队列!")
return
}
for t != nil {
fmt.Printf("%d -> ", t.Value)
t = t.Next
}
fmt.Println()
}
func main() {
queue = nil
// 入队
Push(queue, 10)
fmt.Println("Size:", size)
// 遍历
traverse(queue)
// 出队
v, b := Pop(queue)
if b {
fmt.Println("Pop:", v)
}
fmt.Println("Size:", size)
// 批量入队
for i := 0; i < 5; i++ {
Push(queue, i)
}
// 再次遍历
traverse(queue)
fmt.Println("Size:", size)
// 出队
v, b = Pop(queue)
if b {
fmt.Println("Pop:", v)
}
fmt.Println("Size:", size)
// 再次出队
v, b = Pop(queue)
if b {
fmt.Println("Pop:", v)
}
fmt.Println("Size:", size)
// 再次遍历
traverse(queue)
}
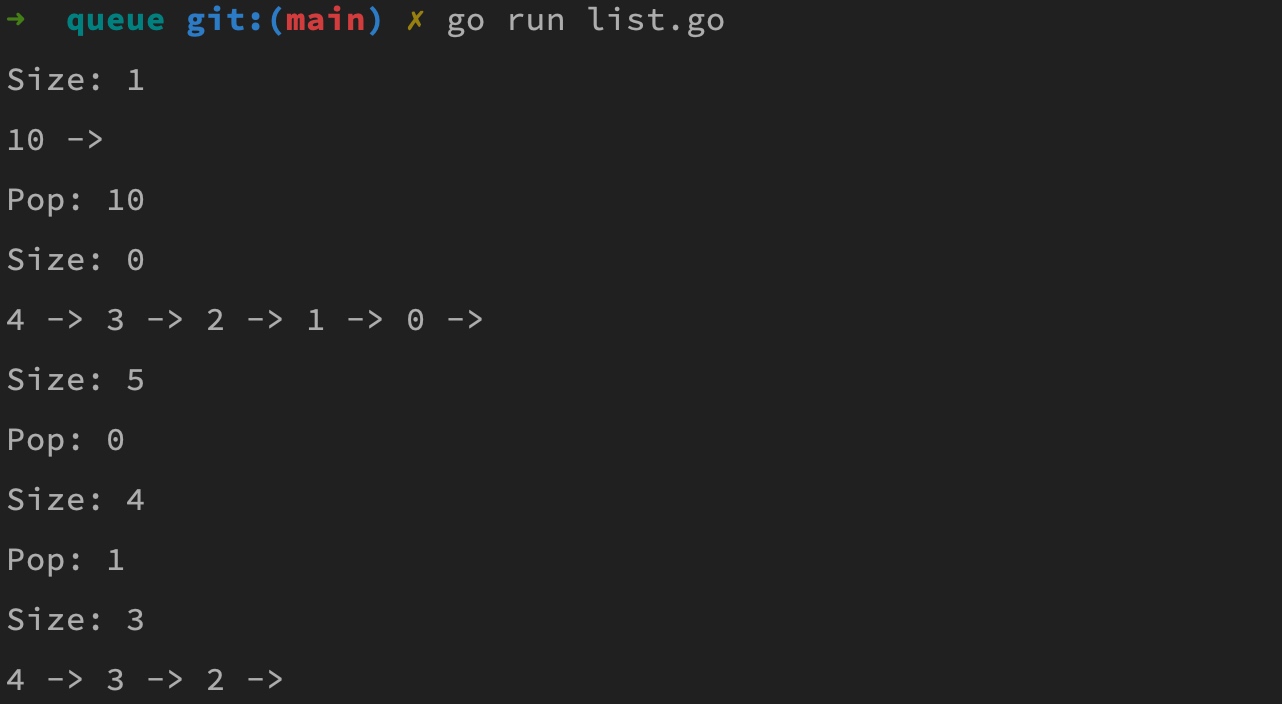
除了入队出队位置和栈不同外,其他代码实现很相似。运行上述代码,打印结果如下:
基于数组实现队列存在的问题
如果通过数组实现顺序队列的话,有一个问题,就是随着队列元素的插入和删除,队尾指针和队头指针不断后移,从而导致队尾指针指向末尾无法继续插入数据,这时候有可能队列头部还是有剩余空间的,如下图所示:
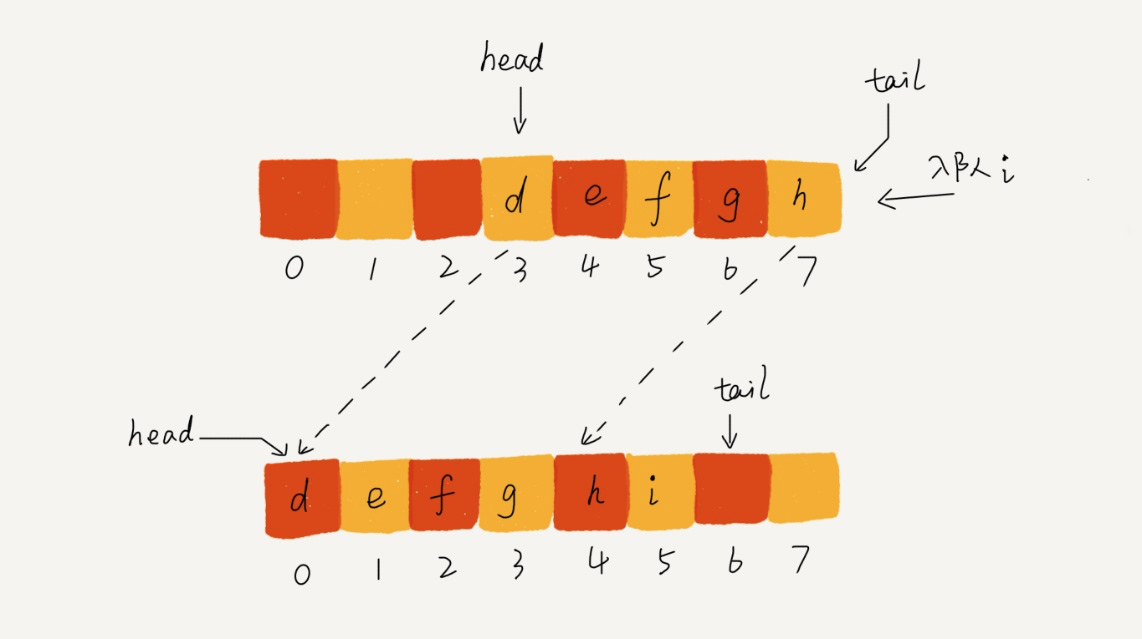
我们当然可以通过数据搬移的方式把所有队列数据往前移,但这会增加额外的时间复杂度,如果频繁操作数据量很大的队列,显然对性能有严重损耗,对此问题的解决方案是循环队列,即把队列头尾连起来:
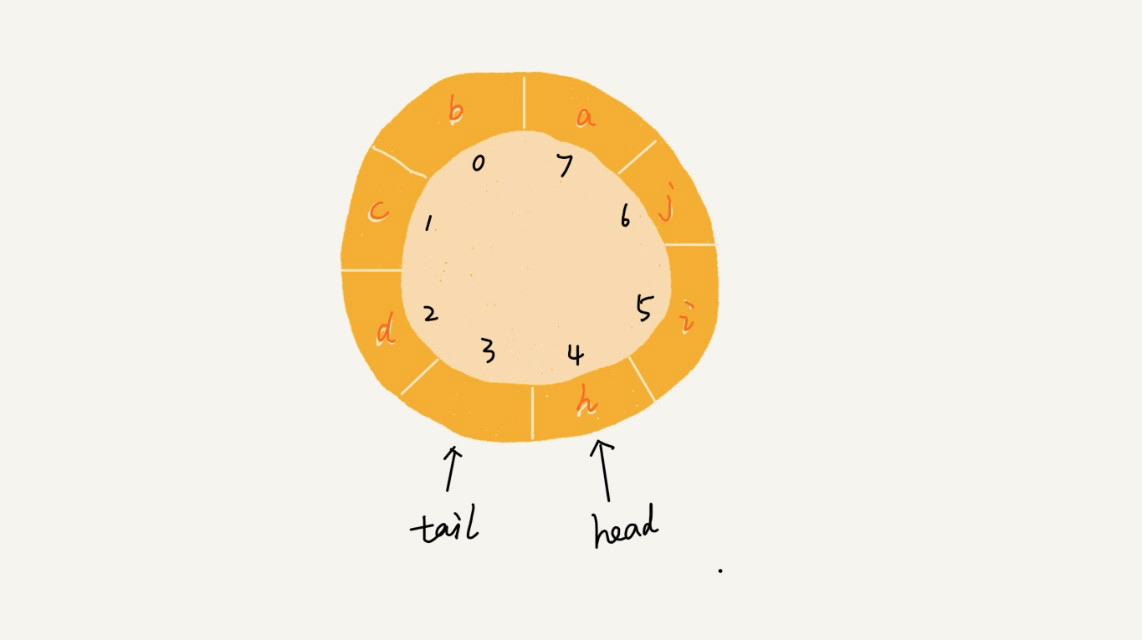
这样一来就不会出现之前的问题了。此时判断队列是否为空的条件还是 tail==head,但是判断队列是否满的条件就变成了 (tail+1) % maxsize == head,maxsize 是数组的长度,浪费一个空间是为了避免混淆判断空队列的条件。
当然如果通过链表来实现队列的话,显然没有这类问题,因为链表没有空间限制。
队列的使用场景
队列的使用也非常广泛,比如我们在业务系统中经常看到的消息队列系统(如 RabbitMq、Kafka、RocketMq 等)就是队列的典型应用场景。



代码注释中 出队应该是队头删除 入队是队尾进入 院长
这看代码 没毛病呀
队列 是应该分为队头和队尾 出队和入队那里 写的没怎么看懂